Normalisation is a process by which we can decompose or divide any relation into more than one relation to remove anomalies in relational database.
It is a step by step process and each step is known as Normal Form.
Normalisation is a reversible process.
1. Benefits of Normalisation
The benefits of normalisation include
- Normalisation produces smaller tables with smaller rows, this means more rows per page and hence less logical I/O.
- Searching, sorting, and creating indexes are faster, since tables are narrower, and more rows fit on a data
- The normalisation produces more tables by splitting the original Thus there can be more clustered indexes and hence there is more flexibility in tuning the queries.
- Index searching is generally faster as indexes tend to be narrower and shorter.
- The more tables allow better use of segments to control physical placement of data.
- There are fewer indexes per table and hence data modification commands are faster.
- There are small number of null values and less redundant This makes the database more compact.
- Data modification anomalies are reduced.
- Normalization is conceptually cleaner and easier to maintain and change as the needs change.
2. Various Normal Forms
The different normal forms are as follows. Each of which has its importance and are more desirable than the previous one.
2.1. First Normal Form (1NF)
A relation is in first normal form if domain of each attribute contains only atomic values. It means atomicity must be present in relation.
Consider the relation Employee as shown in Figure 6.8. It is not in first normal form because attribute Name is not atomic. So, divide it into two attributes First Name and Last Name as shown in Figure 6.9.
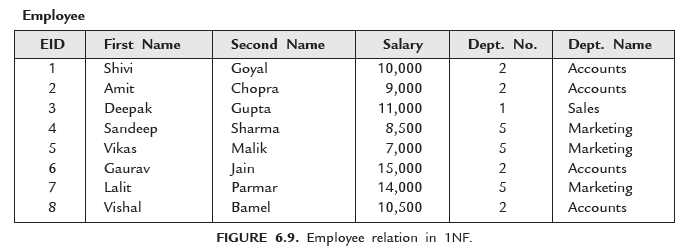
Now, relation Employee is in 1NF.
Anomalies in First Normal Form : First Normal form deals only with atomicity. Anomalies described earlier are also applicable here.
Example. Given the relation PART (Part_ID, Descr, Price, Comp_ID, No) having the following dependencies
Part_ID → Descr
Part_ID → Price
Part_ID, Comp_ID → No
Determine the highest normal form of this relation.
Sol. There exists multi-value attributes. The attributes Comp_ID and No are not determined by the primary key. Hence the relation is not in INF.
2.2. Second Normal Form (2NF)
A relation is in second normal form if it is in 1NF and all non-primary key attributes must be fully functionally dependent upon primary key attributes.
Consider the relation Student as shown in Figure 6.10(a) :

The Primary Key is (RollNo., Game). Each Student can participate in more than one game.
Relation Student is in 1NF but still contains anomalies.
- Deletion anomaly : Suppose you want to delete student Here you loose information about game Hockey because he is the only player participated in hockey.
- Insertion anomaly : Suppose you want to add a new game Basket Ball having no student participated in You cannot add this information unless there is a player for it.
- Updation anomaly : Suppose you want to change Fee of Cricket. Here, you have to search all the students participated in cricket and update fee individually otherwise it produces inconsistency
The solution of this problem is to separate Partial dependencies and Fully functional dependencies. So, divide Student relation into three relations Student(RollNo., Name), Games (Game, Fee) and Performance(RollNo., Game, Grade) as shown in Figure 6.11.
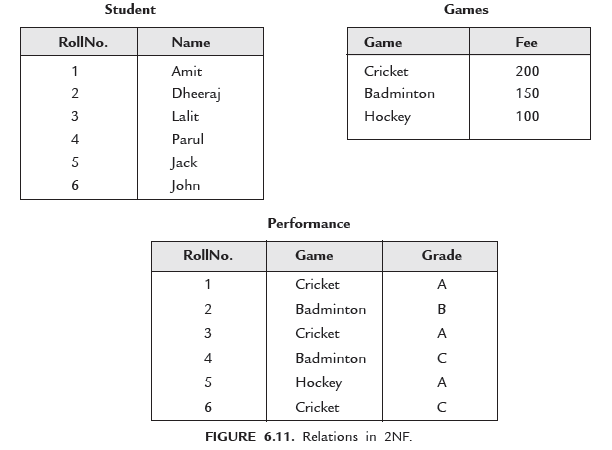
Now, Deletion, Insertion and updation operations can be performed without causing inconsistency.
2.3. Third Normal Form (3NF)
A relation is in Third Normal Form if it is in 2NF and non-primary key attributes must be non-transitively dependent upon primary key attributes.
In other words a relation is in 3NF if it is in 2NF and having no transitive dependency. Consider the relation Student as shown in Figure 6.12(a).
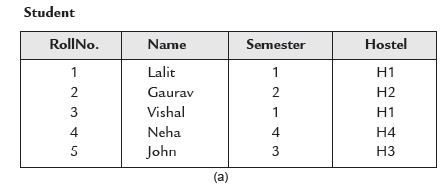
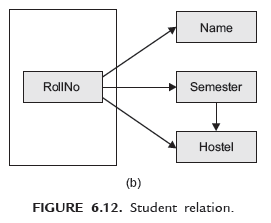
The Primary Key is (RollNo.). The condition is different Hostel is allotted for different semester. Student relation is in 2NF but still contains anomalies.
- Deletion anomaly : If you want to delete student You loose information about Hostel H2 because he is the only student staying in hostel H2.
- Insertion anomaly : If you want to add a new Hostel H8 and this is not allotted to any You cannot add this information.
- Updation anomaly : If you want to change hostel of all students of first You have to search all the students of first semester and update them individually otherwise it causes inconsistency.
The solution of this problem is to divide relation Student into two relations Student(RollNo.Name, Semester) and Hostels(Semester, Hostel) as shown in Figure 6.13.

Now, deletion, insertion and updation operations can be performed without causing inconsistency.
Example. Given the relation BANK (Account#, Cust_No, Cust_Name, Balance). Determine whether the relation is in 1NF, 2NF, 3NF or unnormalizd. If it is not in 3NF, convert it into 3NF relations.
Sol. Since there does not exist multi-value attributes, hence the relation is at least 1NF.
- There does not exist any partial dependency as the primary key has only one
- There exists a transitive dependency
i.e. Cust_No → Cust_Name
Hence the relation is not in 3NF. To convert this relation into 3NF, make a new relation CUSTOMERS with attributes Cust_Name and Cust_No on which it depends. Therefore, the relations in 3NF are CUSTOMERS (Cust_No, Cust_Name) BANK (Account#, Cust_No, Balance).
Example. Given the dependency diagram shown in Figure 6.14. The primary key attributes are underlined.
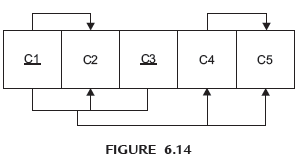
- Identify and discuss each of the indicated dependencies.
- Create a database whose tables are at least in 3NF, showing dependency diagram for each table.
Sol.
- There exists a partial dependency C1 → C2, since C2 depends only on C1 rather than on the entire primary key (C1, C3).
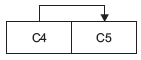
- There exists a transitive dependency C4 →C5, since C5 depends on the attribute C4, which is not a part of the primary
- There exists a functional dependency C1, C3→ C2, C4, C5, since C2, C4, and C5 depend on the primary key (C1, C3).
- The given relation is decomposed into 3NF and the obtained relations are as follows with their dependency diagrams.
- R1 (C1, C2) with FD {C1 ® C2}. The functional dependency diagram is as follows.
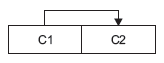
- R2 (C1, C3, C4) with FD {C1, C3 → C4}. The FD diagram is as

- R3 (C4, C5) with FD {C4 → C5}. The FD diagram is as
2.3.1. Synthesis Algorithm for Third Normal Form Decomposition
We can always find a third normal form decomposition of a relation that is lossless and that preserves dependencies. The algorithm for the third normal form decomposition is
Algorithm: To find a lossless join and FD-preserving 3NF decomposition of R
Input: Given a universal relation R and a set of functional dependencies, F, on R,
Output: A lossless join and FD-preserving 3NF decomposition of R
- Calculate the minimal cover of F; call it G (Combine all FDs with same LHS into one FD using “union” rule of inference). Also compute the candidate keys for R.
- For each FD X → Y in G, generate a relation schema XY in the decomposition.
- If there are some attributes, say Z, of R that do not appear in any decomposed schema, then create a separate schema in the decomposition for Z.
- If none of the decomposed schemes contain a candidate key, create a separate schema in the decomposition for one of the candidate keys K.
Example. Consider a relation schema with attributes R = ABCGWXYZ and the set of dependencies
𝐹 = {XZ → ZYB, YA → CG, C → W, B → G, XZ → G}.
- Find a minimal cover for 𝐹.
- Decompose R into a join-lossless 3NF database
Sol.
- The minimal cover for F is as follows: After right-reducing, we have
XZ → B
XZ → G
XZ → Y
YA → C
YA → G
C → W
B → G
It is easy to see that the left-hand sides XZ and YA (as well as C and B) cannot be reduced because there are no FDs of the form X → …, Y → …, Z → …, and A → … .
Further, XZ → G is redundant and none of the others. So, the minimal cover consists of the above set minus XZ → G.
- A join-lossless 3NF decomposition is as follows:
D = {XZBY, YACG, CW, BG, XZA} is a join-lossless 3NF database schema. Note that XZA is added because no other table in D that contains a key of R.
Example. Consider R(ABCDEF) and the following FDs
F = {A → BCE, B → DE, ABD → CF, AC → DE}.. Find a 3NF database for R under F.
Sol.
- The minimal cover for F is as follows: After Left Reduction:
Rule ABD → CF becomes A → CF
Rule AC → DE becomes A → DE
F = {A → BCE, B → DE, A → CF, A → DE}
After Right Reduction:
Rule A → BCE becomes A → B
Rule A → DE becomes A → E
F = {A → B, B → DE, A → CF, A → E}
After Removing Redundant Rule(s):
Rule A → E is redundant (Transitivity on A → B, B → E)
F = {A → B, B → DE, A → CF}.
Therefore, a minimal cover is
F = {A → BCF, B → DE}
- Thus, D = (ABCF, BDE) is a join-lossless 3NF database schema.
2.4. Boyce Codd Normal Form (BCNF)
BCNF is a strict format of 3NF. A relation is in BCNF if and only if all determinants are candidate keys. BCNF deals with multiple candidate keys.
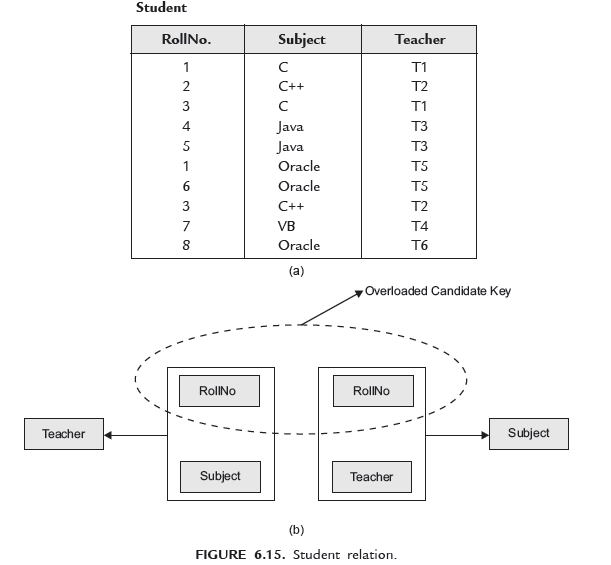
Relations in 3NF also contains anomalies. Consider the relation Student as shown in Figure 6.15(a).
Assumptions:
- Student can have more than 1 subject.
- A Teacher can teach only 1 subject.
- A subject can be taught by more than 1 teacher
There are two candidate keys (RollNo., Subject) and (RollNo., Teacher)
Relation Student is in 3NF but still contain anomalies.
- Deletion anomaly : If you delete student whose is 7. You will also loose information that Teacher T4 is teaching the subject VB.
- Insertion anomaly : If you want to add a new Subject VC++, you cannot do that until a student chooses subject VC++ and a teacher teaches subject VC++.
- Updation anomaly : Suppose you want to change Teacher for Subject You have to search all the students having subject C and update each record individually otherwise it causes inconsistency.
In relation Student, candidate key is overloaded. You can find Teacher by RollNo. and Subject. You can also find Subject by RollNo. and Teacher. Here RollNo. is overloaded. You can also find Subject by Teacher.

The solution of this problem is to divide relation Student in two relations Stu-Teac and Teac-Sub as shown in Figure 6.17.

In this solution all determinants are candidate keys.
2.4.1. Decomposition Algorithm for BCNF with Lossless Join
It is always possible to find a decomposition of a relation that is Boyce-Codd Normal Form and that has the lossless join property. The process involves finding each violation of BCNF and removing it by decomposing the relation containing it into two relations. The process is repeated until all such violations are removed. The algorithm is
Given a universal relation R and a set of functional dependencies on the attributes of R:
- D ← R;
- while there is some relation schema S in D that is not already BCNF
{
-
- Find a functional dependency X→Y in S that violates BCNF
- Replace S by two relation schemas (S–Y) and (X,Y)
}
Example. The relation is R (A, B, C, D, E) and the FD’s : A → E, BC → A and DE → B. Decompose the relation into BCNF with lossless join.
Sol. A you see that {A}+ = {A,E}, violating the BCNF condition. We split R to R1(A,E) and R2(A,B,C,D).
R1 satisfies BCNF now, but R2 not because of: {B,C}+ = {B,C,A}. Notice that the FD, D E → B has now disappeared and we don’t need to consider it! Split R2 to: R2(B,C,A) and R3(B,C,D).
Second Sol. You can split the R differently. Let’s try with the violation {B,C}+ = {B,C,A,E}. We initially split to R1(B,C,A,E) and R2(B,C,D). Now we need to resolve for R1 the violation {A}+ = {A,E}. So we split again R1 to R1(A,E) and R3(A,B,C). The same!
You can also start splitting by considering the BCNF violation {D,E}+ = {D,E,B}. The resulting BCNF decomposition in this case will be a different one.
2.5. Multivalued Dependencies and Fourth Normal Form
Definition: Let R be a relation having attributes or sets of attributes A, B, and C. There is a multivalued dependency of attribute B on attribute A if and only if the set of B values associated with a given A value is independent of the C values.
We write this as A →→ B and read it as A multidetermines B. If R has at least three attributes, A, B, and C then in R(A, B, C), if A →→ B, then A→→ C as well.
Alternate definition of Multivalued Dependency
More generally, if R is a relation with multivalued dependency A →→ B
then in any table for R, if two tuples, t1 and t2, have the same A value, then there must exist two other tuples t3 and t4 obeying these rules
- t3 and t4 have the same A value as t1 and t2
- t3 has the same B value as t1
- t4 has the same B value as t2
- If R – B represents the attributes of R that are not in B, then the t2 and t3 have the same values for R – B and
- t1 and t4 have the same values for R – B
The dependency A →→ B is called a trivial multivalued dependency if B is a subset of A or A ∪ B is all of R. Now we are ready to consider fourth normal form.
Definition: A relation is in fourth normal form (4NF) if and only if it is in BoyceCodd normal form and there are no nontrivial multivalued dependencies.
Fourth Normal Form (4NF)
A relation is in 4NF if it is in BCNF and for all Multivalued Functional Dependencies (MVD) of the form X →→ Y either X → Y is a trival MVD or X is a super key of relation.
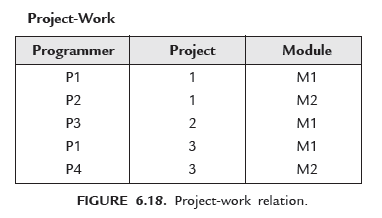
Relations in BCNF also contains anomalies. Consider the relation Project-Work as shown in Figure 6.18.
Assumptions:
- A Programmer can work on any number of projects.
- A project can have more than one module.
Relation Project-work is in BCNF but still contains anomalies.
- Deletion anomaly : If you delete project You will loose information about Programmer P3.
- Insertion anomaly : If you want to add a new project You cannot add this project until it is assigned to any programmer.
- Updation anomaly : If you want to change name of project Then you have to search all the programmers having project 1 and update them individually otherwise it causes inconsistency.
Dependencies in Relation Project-work are
Programmer →→ Project
Project →→ Module
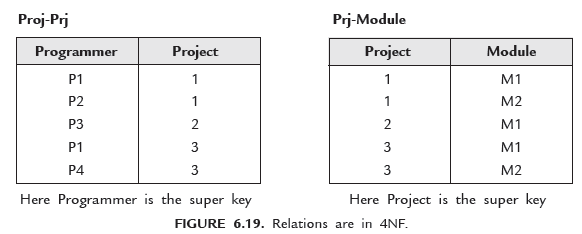
The solution of this problem is to divide relation Project-Work into two relations Prog-Prj (Programmer, Project) and Prj-Module (Project, Module) as shown in Figure 6.19.
2.6. Projection Join Normal Form (5NF) and Join Dependency
Join Dependency : Let R be a given relation upto 4NF and it decompose (Projected or divided) into {R1, R2, R3, …, Rn}. The relation R satisfy the join dependency * {R1, R2, R3, … Rn} if and only if joining of R1 to Rn = R.
Consider the Relation XYZ with attributes X# (Customer_ID), Y# (Account_ID) and Z# (Branch_ID) as shown in Figure 6.20.
First, decompose XYZ into three relations XY, YZ and ZX.
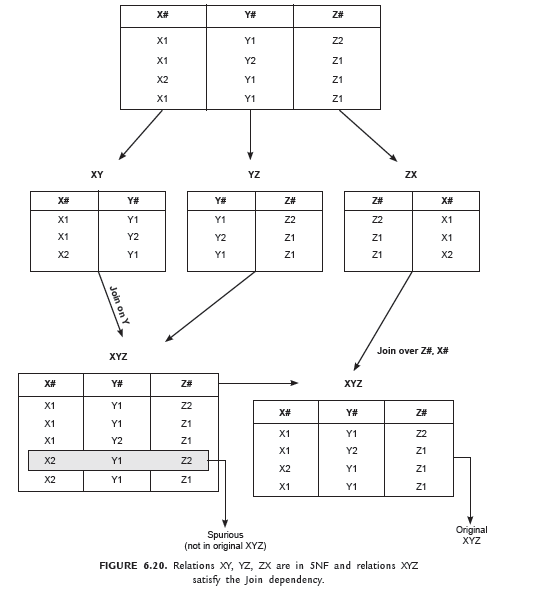
When joined, these three relations give original form of XYZ. So relation XYZ satisfy the join dependency.
Deflnition Projection Join Normal Form (5NF) : Let R is a relation and D is a set of all dependencies (Multivalued dependency, Functional dependency, Join dependency etc.) The relation R is in 5NF w.r.t. D if every Join Dependency is trivial.
Or
A table is in fifth normal form (5NF) or Project-Join Normal Form (PJNF) if it is in 4NF and it cannot have a lossless decomposition into any number of smaller tables.
Properties of 5NF: The following are the properties of 5NF
- Anomalies can occur in relations in 4NF if the primary key has three or more fields.
- 5NF is based on the concept of join dependence – if a relation cannot be decomposed any further then it is in 5NF.
- Pairwise cyclical dependency means that:
- You always need to know two values (pairwise).
- For any one you must know the other two (cyclical).
5NF is the ultimate Normal form. A relation in 5 NF is guaranteed to be free of anomalies. Consider the example in Figure 6.20, where relations XY, YZ and ZX are in 5NF.
Example. Consider the following Buying table. This table is used to track buyers, what they buy, and from whom they buy? Take the following sample data:
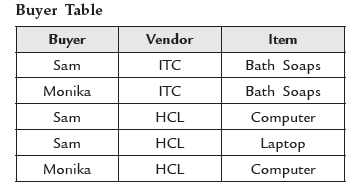
The problem with the above table is that if HCL starts to sell computers then how many records must you create to record this fact? The problem is there as there are pair- wise cyclical dependencies in the primary key. That is, in order to determine the item you must know the buyer and vendor, and to determine the vendor you must know the buyer and the item, and finally to know the buyer you must know the vendor and the item.
The solution is to break this one table into three tables; BuyerVendor table, BuyerItem table and VendorItem table. All these three tables are in the 5NF.


2.7. 6NF or Domain-Key Normal Form (DKNF)
A table is in sixth normal form (6NF) or Domain-Key normal form (DKNF) if it is in 5NF and if all constraints and dependencies that should hold on the relation can be enforced simply by enforcing the domain constraints and the key constraints specified on the relation.
The domain-key normal form (DKNF) is a theoretical statement of how relationships are formed between tables.
Source: Gupta Satinder Bal, Mittal Aditya (2017), Introduction to Basic Database Management System, 2nd Edition-University Science Press (2017)